K-최근접 이웃(KNN) 알고리즘이란? - 1. 개념 설명

소개

K 근접 이웃 분류 알고리즘은 그 단순함에도 불구하고 회귀 분석에 밀려나 기계학습 교과서 중간쯤으로 물러나 있는 것을 확인할 수 있을 것이다. 사실 컴퓨터 비전의 관점에서는 굉장히 단순 무식한 방법이고, 더 단순한 데이터를 상대로는 서포트 벡터 머신(SVM) 같이 평균적으로 더 관측 개체들을 분류 잘하는 알고리즘도 있지만 단순하다고 무시하기에는 굉장히 유용하고 비교적 이해하기 쉬운 알고리즘이다. 맨날 지겹도록 다루는 회귀 분석 말고 좀 더 색다른 알고리즘부터 먼저 보고 싶어 하는 여러분을 위해 일단 해당 알고리즘부터 다뤄보도록 하겠다. 일단 동기 부여부터 시작해보자.

여러분에게 다음과 같은 관측 개체들이 들어간 그림이 주어졌다고 하자. 해당 그림에는 '+' 그룹과 '-' 그룹이 들어가 있다. Scikit Learn 패키지에 내장되어 있어 KNN 설명에 많이 사용되는 꽃의 독특한 특징에 따라 3가지 종으로 분류될 수 있는 150개의 붓꽃(Iris) 데이터에 맞춰 비유를 해보자. y-축을 꽃잎의 길이 그리고 x-축을 꽃잎의 너비라고 생각하고, '+' 그룹은 Setosa 종, '-' 그룹은 Virginica 종에 해당된다고 생각하면 응용적인 면에서 더 이해하기 쉬울 것이다.

그림 1

이에 더해서 새로운 데이터가 관측되었을 때 여러분이 다음 두 가지 사례에서 새 데이터를 '+' 그룹과 '-' 그룹 둘 중 하나로 나누는 방법은 무엇일까? 그림에 새로 추가된 초록색 점을 보고 어느 그룹에 해당되는지 생각해보자.

그림 2

필자는 여러분이 점이 어느 그룹에 가까운지 보고 분류할 것이라고 생각한다. 이 '가깝다'라는 개념을 수학적으로 어떻게 표현할까? 이를 위한 다양한 거리가 존재하긴 하나 KNN 알고리즘은 보통 유클리드 거리로 이 가까움의 개념을 수용한다. 유클리드 거리는 여러분에게 매우 친숙한 개념이라고 장담한다. 우리가 지금 보고 있는 2차원에서 두 점 $p = (p_0, p_1), q = (q_0, q_1)$가 주어졌을 때 유클리드 거리는 다음과 같이 정의된다.

$$\sqrt{(p_0 - q_0)^2 + (p_1 - q_1)^2}$$

그렇다. 우리가 중학교부터 지겹게 봐왔던 그래프 위의 두 점 사이의 거리다. 실생활에서 우리는 이 정의를 더욱 친숙한 형태로 보게 되는데 우리는 그것을 피타고라스 정리라고 부른다.^[각주:1] 그러나 우리가 실제로 보게 될 데이터들은 단순히 2가지 피쳐(feature)^[각주:2]들로만 한정되지는 않을 것이다. 예를 들면 집값 예상을 위해 사용되는 집의 특징이 몇 개나 있는지 생각해보자. 2개 정도로는 정확한 예상은 어림도 없을 것이다. 이런 상황들을 위해 사용하는 다차원으로 일반화된 유클리드 거리의 정의는 다음과 같다.

$$\sqrt{\sum_{i=0}^{n} (p_i - q_i)^2}$$

그러나 꼭 이렇게 눈으로만 분류하기 쉽게 데이터가 등장하지는 않는다. 만약 새로 관측된 데이터가 '+' 그룹과 '-' 그룹 사이에 애매하게 걸쳐져 있다면 어떻게 분류해야 될까? K 근접 이웃 알고리즘은 이를 다수결 투표로 정하는 룰을 만들어서 해결한다. 다시 말하자면, 해당 데이터에 유클리드 거리상 가장 가까운 K개의 점들이 어느 그룹에 포함되는지에 따른 과반수 투표로 정한다. 예를 들어, K가 3일 때 가장 가까운 3개의 점들이 '+' 그룹이 2개 그리고 '-' 그룹이 1개라면 K 근접 이웃 알고리즘은 해당 데이터를 '+'그룹으로 분류할 것이다.

한계 및 보완

여기서 좀 더 생각을 해본다면 다수결이라는 사실에서 발생하는 기술적인 문제들이 떠오를 것이다. 투표가 과반수 이상이 아니고 정확히 일치하는 상황이 나온다면 어떻게 해결해야 될까? 보통은 그런 상황을 회피하기 위해 2개의 클래스로 분류하는 경우에는 K를 홀수로 정한다. 3개의 클래스로 넘어간다면 이것도 안 통할 수 있다. 이런 상황을 타개하기 위한 여러 가지 해결책들이 있다.

• 데이터에서 가장 많이 관측되는 클래스로 분류한다. 예를 들어 우리가 가진 데이터에 '+' 그룹이 많으면 '+'로 분류한다.

• K를 1로 변경하고 해당 데이터를 다시 분류해준다. 그러니까 제일 가까운 한 점이 속해있는 클래스로 분류해준다.

• 클래스를 랜덤으로 분류해준다.

여기에 더해 측정 단위를 무엇으로 정의했느냐에 따라서 손쉽게 분류가 바뀌어 버릴 수도 있다. 간단한 예를 들어 설명해보겠다. 당신에게 해당 데이터 $(1, 5), (4, 4), (2, 6)$가 주어졌다고 해보자. 이때 $(4, 4)$는 유클리드 거리상으로 $(2, 6)$에 더 가깝다. 여기서 $y$값의 비율을 유지시키면서 단위를 1000배로 높여보자. 이때는 반대로 $(4, 4000)$이 $(1,5000)$에 더 가까운 것을 목격할 수 있다. 여기서 왜 이런 일이 일어났는지 더 깊이 이해하고자 한다면 다음 일반화를 참고하자.

데이터들의 $x$값, $y$값 간의 차이들의 절댓값을 임의로 $a, b, c, d$라고 부르겠다. 앞서 언급한 유클리드 거리 예에서는 다음과 같은 관계가 형성된 것을 볼 수 있었다. 루트로 인해서 양의 실수($\mathbb{R}^+$)들의 부등호 관계가 변경되는 일은 없으므로 편의를 위해 루트 표기는 생략하도록 하겠다. 

$$a^2 + b^2 = 2^2 + 2^2 < c^2 + d^2 = 3^2 + 1^2$$

여기서 우리는 $d, b$를 1,000으로 곱했다. 이는 $d$가 보다 $b$ 큰 것을 극대화시켜 $c$가 $a$보다 큼이 전체 셈에 미치는 영향을 비교적 작게 만들어 부등호를 다음과 같이 변경시켜 버린 것이다. 

$$a^2 + (1000b)^2 = 2^2 + 2000^2 > c^2 + (1000d)^2 = 3^2 + 1000^2 $$

이와 별개로 정규화(normalization)를 했느냐 안 했느냐에 따라 데이터가 KNN에 올바르게 분류되는지가 정해지기도 한다. 다음 사례를 참고해보자. 여기서 $x_1$ 피쳐 값들은 $x_2$ 피쳐 값들에 비해 굉장히 범위(range)가 좁기 때문에 정규화 전에 다음과 같이 KNN 알고리즘에 의해 제대로 분류가 안되기도 한다. 앞서 말한 측정 단위 사례처럼 계산되는 유클리드 거리가 $x_1$ 피쳐 값들에 의해 받는 영향이 상대적으로 너무나 적기 때문에 사실상 KNN 알고리즘이 $x_2$ 피쳐에서만 분류를 위한 의미있는 정보를 얻고 있는 것이다.

x1 축 정규화 전

 

x1축 정규화

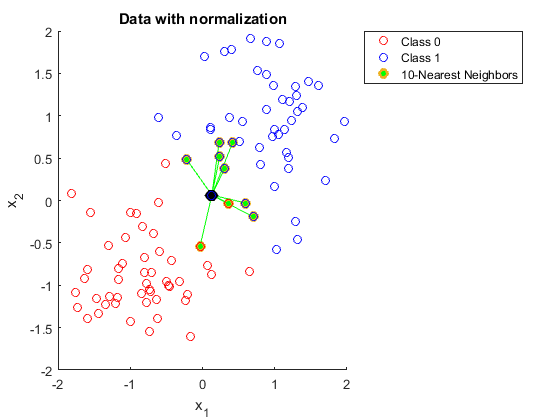
이런 상황이 안 나오도록 우리는 데이터 전처리 과정에서 데이터 스케일링(data scaling)을 혹은 애초부터 단위를 통일시켜 데이터 표준화를 해줘야 한다.

마지막으로 개념 설명에서 눈치챘겠지만 가장 가까운 점들을 찾기 위해 KNN 알고리즘은 새로운 관측의 클래스를 분류해줄 때마다 주어진 모든 훈련 데이터와 유클리드 거리 측정을 해야 되고 그 거리 값들을 최종적으로 순위를 매기기 전까지 저장해야 한다. 이는 메모리를 많이 잡아먹는 과정이고 데이터의 차원이 높아질 때마다 이 현상은 더욱 심화된다.

출처: https://stats.stackexchange.com/questions/287425/why-do-you-need-to-scale-data-in-knn

Why do you need to scale data in KNN

[Copyright ⓒ 블로그채널 무단전재 및 재배포 금지]

1. 이해가 안 간다면 $x$축 값의 차이와 $y$축 값의 차이를 직각삼각형의 변이라고 생각해보자. [본문으로]
2. 우리가 일반적으로 사용하는 '특징'이라는 단어와 혼동되기 때문에 위키피디아에서 사용하는 표기로 쓰도록 하겠다 [본문으로]