| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- 퍼셉트론
- ANOVA
- 딥러닝
- 분산분석
- Bayes Theorem
- knn
- AI
- p 값
- 컴퓨터 조립
- 조건부 확률
- 심층학습
- LeetCode
- 인공지능
- 컴퓨터
- 인공지능 겨울
- 통계
- Bayes Rule
- 확률
- 인공신경망
- AI Winter
- Neural Network
- 편향
- 베이즈 정리
- 30 Day Challenge
- Stack
- p-value
- Today
- Total
군더더기 없는 기계학습 백과사전
파이썬으로 인공신경망(Neural Network) 구현하기(3) 본문
전편에서 주어진 코드를 간략화하기 위해서 Numpy 패키지에서 행렬 연산 기능을 가져왔다. 이제 슬슬 여러 개의 뉴런층을 다루는 수준으로 나아가도록 하자.
우선의 배치(batch)의 개념부터 다뤄보도록 하겠다. 우선 배치 학습을 통한 모델 학습은 데이터를 몇 개로 나눠서 단순한 작업을 여러 코어에 나눠 효율적인 병렬 연산(parallel computing)을 수행하고자 하는 목적도 존재한다. 그러나 배치를 사용하는 또 다른 목적은 우리가 훈련시키고 있는 모델이 (그러니까 지금 우리가 만들고 있는 인공신경망이) 아직 관측한 적이 없는 데이터에 대한 올바른 예측을 수행하도록 도와주는 일반화(generalization) 작업이기도 하다.
여기서 모델을 일반화하는데 도움을 준다는 것은 무슨 뜻일까? 우리의 코드 블럭에 있는 입력값 [2.3, 5.6, 1.2, 2.4]을 어느 회사 서버가 다운되는 일이 없도록 도와주는 여러 센서 장치들을 통해 특정 시점에 기록된 온도, 습도 같은 피쳐(feature) 값이라고 생각해보자. 만약 이런 값들을 어느 시간대에 걸쳐 수집한 데이터가 있다고 했을 때 모델에 데이터 값을 한 개씩 노출시켜 훈련시키기보다는 작은 집합들로 나눈 샘플 집합 혹은 배치로 훈련시켜주면 모델이 보지 못했던 새로운 데이터에 대한 예측 능력은 향상된다. 왜 그런지 이해하기 위해 간단한 선형 회귀 모델로 예를 들어보도록 하자.
여기서 만약 선에게 점을 한개씩 줘서 오차(error)를 줄이도록 명령하면 선은 점 한 개 한 개에 맞춰 기울기를 수정하느라 이리저리 휘둘리고 있을 것이다. 그리고 결국엔 주어진 데이터 점들 전체에 대해 모델의 예측과 실제 데이터의 연속 y값 간의 오차(error)를 최대한 줄이지 못할 것이다.
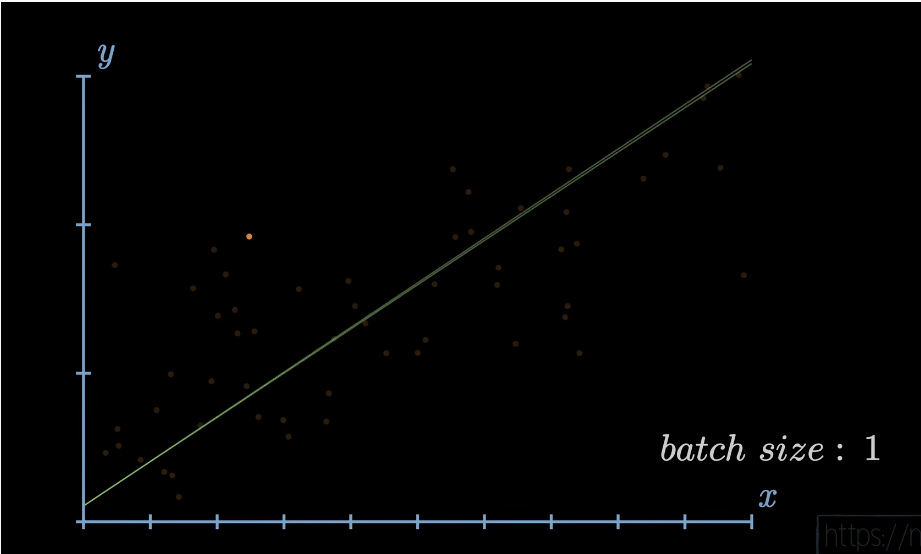
반면 점을 한번에 여러 개씩 주면, 여러분은 선형 회귀 모델의 선이 데이터 전체에 대해 훨씬 정확하게 오차를 줄여나가는 과정을 겪는 것을 볼 수 있을 것이다. 여기서 의문점이 생길지도 모른다. 한 번에 데이터를 다 보여주면 안 될까? 안타깝게도 우리가 실제로 처리해야 하는 데이터는 몇 만개 이상일 수도 있다. 이를 한 번에 다 써서 모델을 훈련시켜버리면 굉장히 오래 걸리고 비효율적인 계산 과정이 일어난다. 특히나 컴퓨터의 연산 처리 능력이 한정된 현실의 상황에서는 배치는 필수적으로 사용해야하는 기법이다. 여기에 더해 모델이 학습 데이터에 과하게 맞아버리는 과적합(overfitting) 현상이 발생하여 표본 외의 데이터 상대로 예측 능력이 떨어지는 모델이 만들어져 오히려 우리가 추구하고자 했던 일반화의 실패가 발생한다.
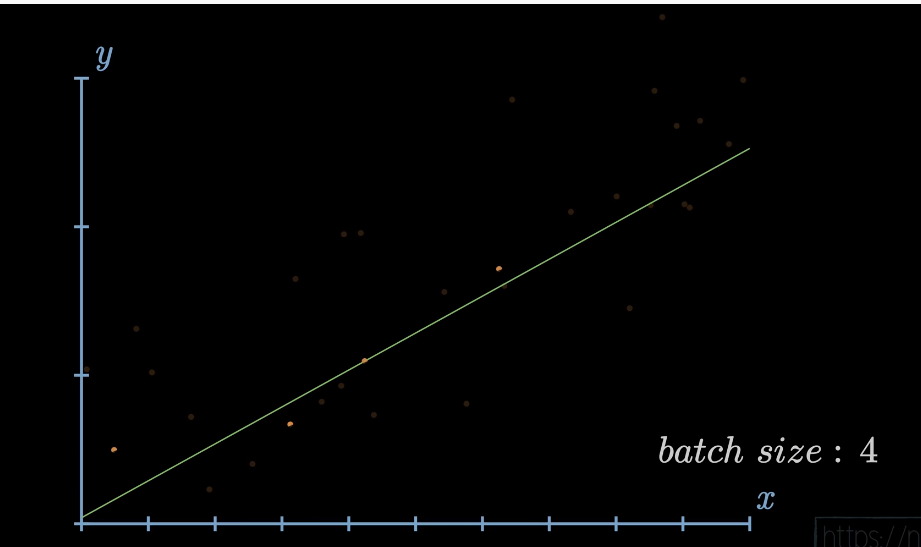
이런 일반화 개념을 인공신경망의 상황에 대입하여 이해하면 된다. 실전에서는 배치 크기가 주로 32 임을 참고하자.
일단 입력값을 배치로 변형시켜보자. 이는 3개의 입력값의 리스트로 이루어진 리스트로 표현하도록 하겠다. 행렬으로 생각하면 행의 갯수 인 3이 배치의 크기에 해당된다.
입력값 = [[2.3, 5.6, 1.2, 2.4],
[1.0, 2.0, 3.0, 2.5],
[2.0, 5.0, -1.0, 2.0]]
가중치 = [[3.1, -2.1, 8.7, -9.1],
[4.5, 2.1, -1.7, 3.4],
[2.3, -6.4, 2.1, -6.3]]
편향 = [2.0, 3.0, 1.0]
출력값 = np.dot(가중치, 입력값) + 편향
print(출력값)여기서 그대로 np.dot 함수를 돌려버리면 우리는 오류가 나버리는 것을 확인할 수 있다. 일단 무슨 일이 일어났는지 좀 더 자세히 알아보도록 하자. np.dot 함수는 인수들의 차원에 따라 다른 행렬 연산 작업을 수행한다.1 여기서 조금 이해하기 힘들 수도 있으므로 차례차례 예를 들어 설명하도록 하겠다. 2편에서는 np.dot(가중치, 입력값)은 다음과 같은 점곱 작업을 수행했다. 첫 번째 인수는 (3,4) 행렬 두 번째 인수는 그냥 크기가 4인 벡터였으므로 출력 값은 크기 3인 벡터로 결정된다. 이 크기 3 벡터의 $a, b, c$ 원소들은 각각 (3,4) 행렬의 행과 크기 4 벡터의 점곱이다.
$$\begin{bmatrix} 3.1 & -2.1 & 8.7 & -9.1 \\ 4.5 & 2.1 & -1.7 & 3.4 \\ 2.3 & -6.4 & 2.1 & -6.3\end{bmatrix} \begin{bmatrix} 2.3, & 5.6 & 1.2 & 2.4 \end{bmatrix} = \begin{bmatrix} a & b & c \end{bmatrix}$$
그러나 이와 달리 np.dot()의 인수들이 2차원 이상의 행렬이면 np.dot() 함수는 행렬 곱셈을 수행한다. 그러니까 dot 함수가 가중치 행렬을 $A$라 하고 입력값 행렬을 $B$라 했을 때 그대로 $AB$ 행렬 곱셈으로 계산해버리기 때문에 $A$ 열수와 $B$의 행수가 맞지 않아 때문에 버그가 발생한 것이다.2 그러나 우리가 진정으로 원하는 연산은 각 행렬의 행 간의 점곱이다. 각 행렬의 원소를 예를 들어 설명하자면 다음과 같은 점곱이다. $$[2.3, 5.6, 1.2, 2.4] \cdot\ [3.1, -2.1, 8.7, -9.1]$$ 만약 헷갈린다면 다시 1편으로 가서 뉴런층 간 이동을 표현하는 연산을 복습하고 오도록 하자.
이 연산을 행렬 곱셈으로 수행하고자 한다면 어떻게 해야 할까? 일단 가중치 행렬을 전치(transpose)해준다. Numpy 패키지에는 이를 위한 함수가 당연히 존재한다. $$\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}^{T} = \begin{bmatrix} 1 & 3 \\ 2 & 4 \end{bmatrix}$$ 가중치 행렬을 전치해주면 np.dot() 우리가 원하는 올바른 연산을 수행해 줄 것이다. 여기서 가중치 리스트를 전치해주기 전에 알아야 할 점들은 파이썬의 리스트 자료구조는 기본적으로 전치라는 메소드(method)가 없다는 점이고 np.dot() 함수는 뒤에서 가중치, 입력값 리스트를 Numpy 배열로 변형시켜주는 작업을 수행한 뒤 행렬 곱셉을 수행한다는 점이다. 따라서 우리는 가중치 리스트를 미리 Numpy 배열로 변형시키고 ". T" 함수를 이용해 전치해준다.
다음으로 np.array(가중치).T와 입력값 인수의 순서를 바꿔준다. 이제 다음 코드 블록은 다음과 같은 행렬 곱셈을 수행할 것이다. 여기서 우리는 (3,3) 행렬을 np.dot() 함수의 출력 값으로 얻을 것이다.
$$\begin{bmatrix} 2.3, & 5.6 & 1.2 & 2.4 \\ 1.0 & 2.0 & 3.0 & 2.5 \\ 2.0 & 5.0 & -1.0 & 2.0\end{bmatrix} \begin{bmatrix}3.1 & 4.5 & 2.3 \\ -2.1 & 2.1 & -6.4 \\ 8.7 & -1.7 & 2.1 \\ -9.1 & 3.4 & -6.3\end{bmatrix}$$
마지막으로 자동으로 편향은 각 행에 따로 더해진다.
입력값 = [[2.3, 5.6, 1.2, 2.4],
[1.0, 2.0, 3.0, 2.5],
[2.0, 5.0, -1.0, 2.0]]
가중치 = [[3.1, -2.1, 8.7, -9.1],
[4.5, 2.1, -1.7, 3.4],
[2.3, -6.4, 2.1, -6.3]]
편향 = [2.0, 3.0, 1.0]
출력값 = np.dot(입력값, np.array(가중치).T) + 편향
print(출력값)이제 은닉층(hidden layer)을 추가해보도록 하자.

해당 층은 노드(node)가 3개다. 이미 익숙한 주어진 코드와 같은 형식으로 코드를 쓰도록 하겠다. 추가된 층에 맞춰서 출력 값 이름도 바꿔주도록 한다.
입력값 = [[2.3, 5.6, 1.2, 2.4],
[1.0, 2.0, 3.0, 2.5],
[2.0, 5.0, -1.0, 2.0]]
가중치 = [[3.1, -2.1, 8.7, -9.1],
[4.5, 2.1, -1.7, 3.4],
[2.3, -6.4, 2.1, -6.3]]
편향 = [2.0, 3.0, 1.0]
가중치2 = [[0.1, -0.14, 0.5],
[-0.5, 0.12, -0.33],
[-0.44, 0.73, -0.13]]
편향2 = [-1.0, 2.0, -0.5]
1층출력값 = np.dot(입력값, np.array(가중치).T) + 편향
2층출력값 = np.dot(1층출력값, np.array(가중치2).T) + 편향2
print(2층출력값)보다시피 새로운 층의 추가와 함께 코드도 복잡해지는 것을 알 수 있을 것이다.
여기까지 왔으면 이제 인공신경망의 기본 단위 작동 방식을 가장 간단한 파이썬 코드를 통해 이해했을 것이라고 생각한다. 다음 편에서는 더 많은 은닉층과 입력값을 단순한 코드로 감당할 수 있도록 파이썬 클래스를 사용하도록 하겠다.
[Copyright ⓒ 블로그채널 무단전재 및 재배포 금지]
- https://numpy.org/doc/stable/reference/generated/numpy.dot.html [본문으로]
- 더 단도직입적으로 말하자면 (3,4) 행렬과 (3,4) 행렬을 행렬 곱셉할 수 없기 때문에 버그가 발생한 것이다. [본문으로]
'Machine Learning > 인공신경망' 카테고리의 다른 글
| 파이썬으로 인공신경망(Neural Network) 구현하기(2) (0) | 2020.04.25 |
|---|---|
| 파이썬으로 인공신경망(Neural Network) 구현하기(1) (1) | 2020.04.21 |


